Inngangur
Í fyrri kafla var sýnt fram á að nákvæmar stærðfræðilegar aðstæður fyrir krafta sem valda kyrrstöðuvökvum væri auðvelt að fá. Þetta er vegna þess að í vatnsstöðu eru aðeins einföld þrýstikraftar í spilinu. Þegar vökvi á hreyfingu er skoðaður verður greiningarvandamálið strax mun erfiðara. Ekki aðeins þarf að taka tillit til stærðar og stefnu agnahraðans, heldur er einnig flókið áhrif seigju sem veldur skerspennu eða núningi milli hreyfandi agna og á mörkum þeirra. Hlutfallsleg hreyfing sem er möguleg milli mismunandi þátta vökvans veldur því að þrýstingur og skerspenna eru töluvert breytileg frá einum punkti til annars eftir flæðisskilyrðum. Vegna flækjustigs sem tengist flæðisfyrirbærinu er nákvæm stærðfræðileg greining aðeins möguleg í fáum, og frá verkfræðilegu sjónarmiði, sumum óframkvæmanlegum, tilvikum. Því er nauðsynlegt að leysa flæðisvandamál annaðhvort með tilraunum eða með því að gera ákveðnar einfaldaðar forsendur sem nægja til að fá fræðilega lausn. Þessar tvær aðferðir útiloka ekki hvor aðra, þar sem grundvallarlögmál aflfræðinnar eru alltaf gild og gera kleift að beita að hluta til fræðilegum aðferðum í nokkrum mikilvægum tilvikum. Einnig er mikilvægt að ákvarða með tilraunum umfang fráviksins frá raunverulegum aðstæðum sem afleiðing af einfaldaðri greiningu.
Algengasta einföldunarforsendan er að vökvinn sé kjörinn eða fullkominn, og þannig útiloki hann flækjandi seigjuáhrif. Þetta er grundvöllur klassískrar vatnsfræði, greinar hagnýtrar stærðfræði sem hefur vakið athygli þekktra fræðimanna á borð við Stokes, Rayleigh, Rankine, Kelvin og Lamb. Það eru alvarlegar innbyggðar takmarkanir í klassísku kenningunni, en þar sem vatn hefur tiltölulega lága seigju, hegðar það sér eins og raunverulegur vökvi í mörgum tilfellum. Af þessari ástæðu má líta á klassíska vatnsfræði sem mjög verðmætan bakgrunn fyrir rannsóknir á eiginleikum vökvahreyfinga. Þessi kafli fjallar um grundvallarhreyfingar vökvahreyfinga og þjónar sem grunninngangur að næstu köflum sem fjalla um sértækari vandamál sem koma upp í byggingarverkfræðivökvafræði. Þrjár mikilvægar grunnjöfnur vökvahreyfinga, þ.e. samfelldni-, Bernoulli- og skriðþungajöfnur, eru leiddar út og þýðing þeirra útskýrð. Síðar eru takmarkanir klassísku kenningarinnar skoðaðar og hegðun raunverulegs vökva lýst. Gert er ráð fyrir óþjappanlegum vökva allan tímann.
Tegundir flæðis
Hægt er að flokka ýmsar gerðir af vökvahreyfingum á eftirfarandi hátt:
1. Ókyrrð og lagskipt
2. Snúnings- og snúningslaus
3. Stöðugt og óstöðugt
4. Einsleitt og ósamleitt.
MVS serían af ásflæðisdælum AVS serían af blandaðri flæðisdælum (lóðréttar ásflæðisdælur og blandaðar flæðisdælur fyrir skólp) eru nútímalegar vörur sem hafa verið hannaðar með því að innleiða erlenda nútímatækni. Afköst nýju dælnanna eru 20% meiri en þeirra gömlu. Nýtni þeirra er 3~5% meiri en þeirra gömlu.

Ókyrrðar- og lagskiptar straumar.
Þessi hugtök lýsa efnislegum eðli flæðisins.
Í ókyrrðarflæði er framvinda vökvaagnanna óregluleg og staðsetningarskipti virðast vera tilviljanakennd. Einstakar agnir eru háðar sveiflum í þversum þannig að hreyfingin er hvirfilbyl og bogadregin frekar en beinlínuleg. Ef litarefni er sprautað inn á ákveðnum stað dreifist það hratt um allan flæðisstrauminn. Í tilviki ókyrrðarflæðis í pípu, til dæmis, myndi tafarlaus skráning á hraðanum á þversniði sýna nálæga dreifingu eins og sýnt er á mynd 1(a). Stöðugur hraði, eins og hann væri skráður með venjulegum mælitækjum, er sýndur með punktalínu og það er augljóst að ókyrrðarflæði einkennist af óstöðugum sveiflum í hraða sem lagður er ofan á tímabundið stöðugt meðaltal.
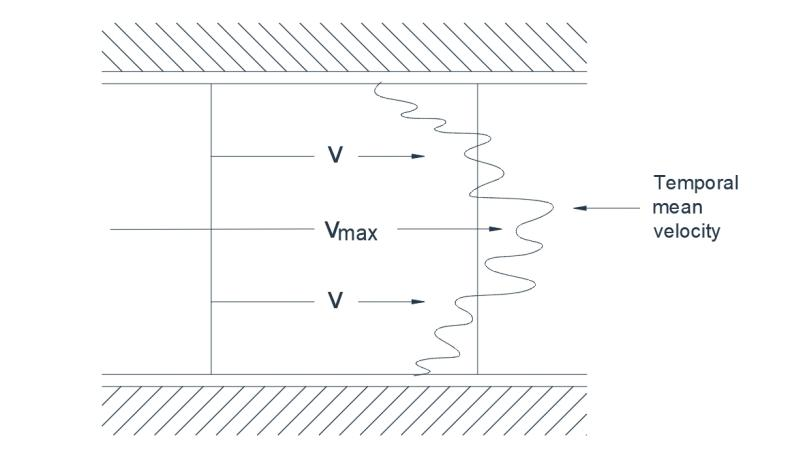
Mynd 1(a) Ókyrrðarflæði
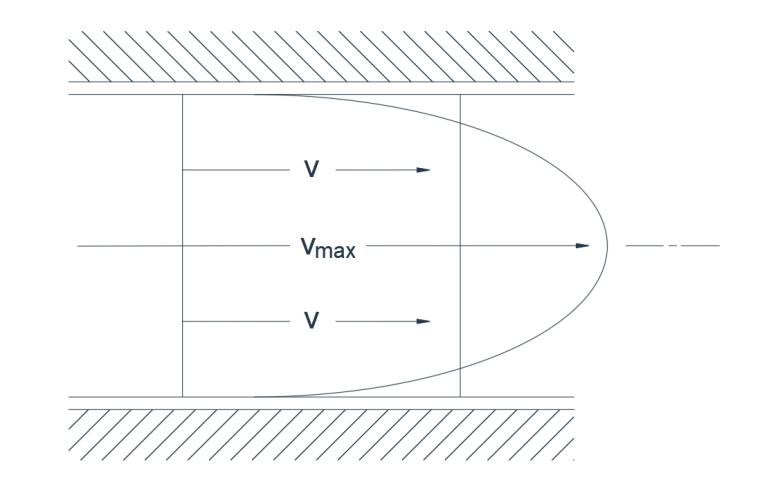
Mynd 1(b) Laminarflæði
Í lagstreymi fara allar vökvaagnir samsíða brautir og það er enginn þversniðsþáttur hraðans. Skipulagða framvindan er þannig að hver ögn fylgir nákvæmlega braut agnarinnar á undan henni án þess að víkja frá. Þannig helst þunnur litarefnisþráður óbreyttur án dreifingar. Þversniðshraðahalli er mun meiri í lagstreymi (Mynd 1b) en í ókyrrðarflæði. Til dæmis, fyrir pípu, er hlutfall meðalhraðans V og hámarkshraðans Vmax 0,5 með ókyrrðarflæði og 0,05 með lagstreymi.
Laminarflæði tengist lágum hraða og seigfljótandi vökva. Í vökvakerfum í leiðslum og opnum rásum eru hraðarnir næstum alltaf nægilega miklir til að tryggja ókyrrðarflæði, þó að þunnt lagskipt lag haldist nálægt föstu mörkum. Lögmál lagskipts flæðis eru að fullu skilin og fyrir einföld jaðarskilyrði er hægt að greina hraðadreifinguna stærðfræðilega. Vegna óreglulegs púlsandi eðlis síns hefur ókyrrðarflæði staðist strangar stærðfræðilegar meðferðir og til að leysa hagnýt vandamál er nauðsynlegt að reiða sig að miklu leyti á empírísk eða hálf-empírísk tengsl.

Gerðarnúmer: XBC-VTP
Lóðréttar, langar ásar slökkviþjónustudælur af gerðinni XBC-VTP eru eins þrepa, fjölþrepa dæludælur með dreifikerfi, framleiddar í samræmi við nýjasta landsstaðalinn GB6245-2006. Við höfum einnig bætt hönnunina með hliðsjón af stöðlum bandarísku slökkvistarfsins. Þær eru aðallega notaðar til að veita slökkvivatn í jarðolíu, jarðgasi, virkjunum, bómullartextíl, bryggjum, flugi, vöruhúsum, háhýsum og öðrum atvinnugreinum. Þær geta einnig verið notaðar í skipum, sjótönkum, slökkviskipum og öðrum atvinnugreinum.
Snúningsflæði og snúningslaust flæði.
Flæði er sagt vera snúningsflæði ef hver vökvaögn hefur hornhraða um eigin massamiðju.
Mynd 2a sýnir dæmigerða hraðadreifingu sem tengist ókyrrðarflæði framhjá beinu mörkum. Vegna ójafnrar hraðadreifingar verður ögn, sem upphaflega er hornrétt á tvær ásar, fyrir aflögun með litlum snúningshraða. Á mynd 2a er flæði í hringlaga
Leiðin er sýnd, þar sem hraðann er í réttu hlutfalli við radíusinn. Ásar agnarinnar snúast í sömu átt þannig að flæðið snýst aftur.
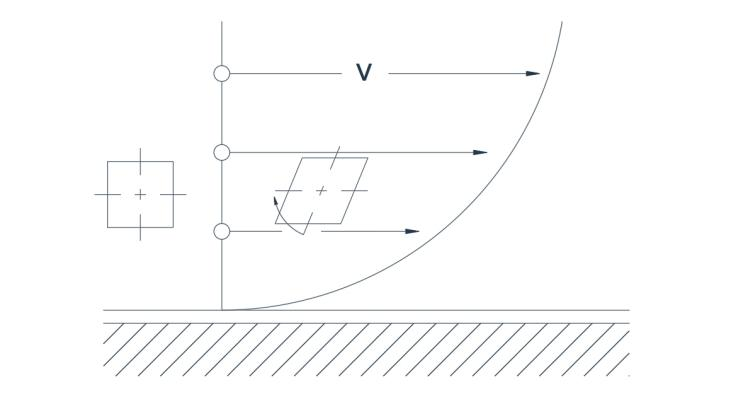
Mynd 2(a) Snúningsflæði
Til þess að flæði sé snúningslaust verður hraðadreifingin aðliggjandi beinu mörkunum að vera einsleit (Mynd 2b). Ef um flæði er að ræða í hringlaga braut má sýna fram á að snúningslaust flæði eigi aðeins við ef hraðinn er í öfugu hlutfalli við radíusinn. Við fyrstu sýn á mynd 3 virðist þetta rangt, en nánari skoðun leiðir í ljós að ásarnir tveir snúast í gagnstæðar áttir þannig að það er jöfnunaráhrif sem veldur meðalstefnu ásanna sem er óbreytt frá upphafsástandi.
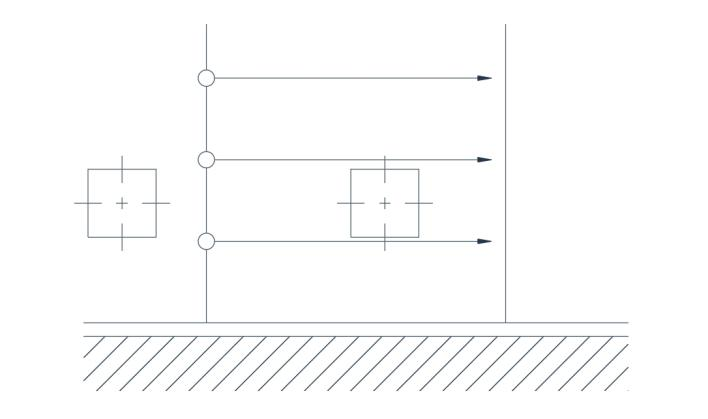
Mynd 2(b) Snúningslaus flæði
Þar sem allir vökvar hafa seigju, þá er lágt gildi raunverulegs vökva aldrei raunveruleg snúningsörvun, og lagstreymi er auðvitað mjög snúningsbundið. Þannig er snúningsörvun tilgáta sem væri aðeins af fræðilegum áhuga ef ekki væri fyrir þá staðreynd að í mörgum tilfellum ókyrrðarflæðis eru snúningseiginleikarnir svo ómerkilegir að þeim má vanrækja. Þetta er þægilegt vegna þess að það er mögulegt að greina snúningsörvun með stærðfræðilegum hugtökum klassískrar vatnsfræði sem vísað er til áður.
Gerðarnúmer: ASN ASNV
ASN og ASNV dælur eru eins þrepa tvísogs miðflótta dælur með klofnu snúningshulsi og notaðar til vökvaflutninga í vatnsveitum, loftræstikerfi, byggingum, áveitu, frárennslisdælustöðvum, raforkuverum, iðnaðarvatnsveitukerfum, slökkvikerfum, skipum, byggingum og svo framvegis.

Stöðugt og óstöðugt flæði.
Flæði er sagt vera stöðugt þegar aðstæður á hverjum tímapunkti eru fastar með tilliti til tíma. Strang túlkun á þessari skilgreiningu myndi leiða til þeirrar niðurstöðu að ókyrrðarflæði hafi aldrei verið sannarlega stöðugt. Hins vegar er í þessu skyni þægilegt að líta á almenna hreyfingu vökvans sem viðmið og óreglulegar sveiflur sem tengjast ókyrrðinni sem aðeins aukaáhrif. Augljóst dæmi um stöðugt flæði er stöðugt rennsli í leiðslu eða opnum rásum.
Afleiðingin er sú að flæði er óstöðugt þegar aðstæður breytast með tímanum. Dæmi um óstöðugt flæði er breytilegt rennsli í leiðslu eða opnum rásum; þetta er venjulega tímabundið fyrirbæri sem kemur í kjölfar stöðugs rennslis. Aðrar kunnuglegar
Dæmi af reglulegri eðli eru ölduhreyfingar og hringlaga hreyfing stórra vatnsfalla í sjávarfallaflæði.
Flest hagnýt vandamál í vatnsfræði snúast um stöðugt flæði. Þetta er heppilegt, þar sem tímabreytan í óstöðugu flæði flækir greininguna verulega. Þess vegna verður óstöðugt flæði í þessum kafla takmarkað við fáein tiltölulega einföld tilvik. Mikilvægt er þó að hafa í huga að nokkur algeng tilvik óstöðugs flæðis má draga niður í stöðugt ástand með því að nota meginregluna um hlutfallslega hreyfingu.
Þannig má umorða vandamál sem felur í sér skip sem siglir í kyrrstöðu vatni þannig að skipið sé kyrrstætt en vatnið sé á hreyfingu; eina skilyrðið fyrir líkingu í hegðun vökva er að hlutfallshraðinn sé sá sami. Aftur má draga úr bylgjuhreyfingu í djúpu vatni í
stöðugt ástand með því að gera ráð fyrir að athugandi ferðast með öldunum á sama hraða.

Lóðrétt frárennslisdæla með dísilvél, fjölþrepa miðflótta dælu með línuás. Þessi tegund af lóðréttri frárennslisdælu er aðallega notuð til að dæla skólpvatni án tæringar, með hitastig undir 60°C og sviflausnum (að undanskildum trefjum og grjóti) sem innihalda minna en 150 mg/L. Lóðrétt frárennslisdæla af gerðinni VTP er notuð í lóðréttum vatnsdælum af gerðinni VTP. Smurolían er stillt á vatnssmurefni miðað við aukningu og kraga. Hægt er að senda skólpvatnið til að innihalda ákveðin föst efni (eins og járnbrot, fínan sand, kol o.s.frv.) ef hitastigið er undir 60°C.
Jafnt og ójafnt flæði.
Flæði er sagt vera einsleitt þegar engin breyting er á stærð og stefnu hraðavigursins frá einum punkti til annars eftir straumleiðinni. Til að uppfylla þessa skilgreiningu verða bæði flatarmál straumsins og hraðinn að vera sá sami í hverju þversniði. Ójafnt flæði á sér stað þegar hraðavigurinn breytist eftir staðsetningu, dæmigert dæmi er flæði milli samleitna eða fráhverfra marka.
Báðar þessar mismunandi flæðisskilyrði eru algeng í opnum rásarvökvafræði, þó strangt til tekið, þar sem einsleitt flæði er alltaf nálgast með asymptotískum hætti, sé það kjörástand sem aðeins er nálgað en aldrei náð í raun. Taka skal fram að skilyrðin tengjast rúmi frekar en tíma og því eru þau, í tilvikum lokaðs flæðis (t.d. í pípum undir þrýstingi), alveg óháð því hvort flæðið er stöðugt eða óstöðugt.
Birtingartími: 29. mars 2024
 sales@tkflow.com
sales@tkflow.com 
